Math

Supported platforms:
Available since: Gideros 2011.6

Description

math table holds most commonly used math functions and constants.

Example

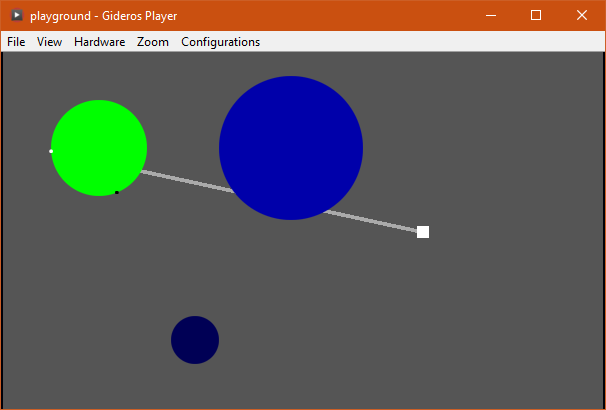
A nice example demonstrating various Gideros specific maths functions

local myappwidth = application:getContentWidth()
local myappheight = application:getContentHeight()
application:setBackgroundColor(0x555555)

local pixel = Pixel.new(0xffffff, 1, 16, 16)
pixel:setAnchorPoint(0.5, 0.5)
pixel:setPosition(7*myappwidth/10, 5*myappheight/10)
stage:addChild(pixel)

local raycast = Shape.new()
stage:addChild(raycast)

-- circle
local p=Particles.new()
stage:addChild(p)
local circlepts={}
circlepts[#circlepts+1] = { -- 1st circle
	x=128, y=128,
	size=128,
	color=0x0000ff,
	id=#circlepts+1,
	radius=128/2,
}
circlepts[#circlepts+1] = { -- 2nd circle
	x=128*3, y=128,
	size=128*1.5,
	color=0x0000aa,
	id=#circlepts+1,
	radius=128*1.5/2,
}
circlepts[#circlepts+1] = { -- 3rd circle
	x=128*2, y=128*3,
	size=64,
	color=0x000055,
	id=#circlepts+1,
	radius=64/2,
}
p:addParticles(circlepts)

-- markers
local pedge = p:addParticles{ {x=0, y=0, size=5, color=0x0} }[1]
local pray = p:addParticles{ {x=0, y=0, size=5, color=0xffffff, alpha=1} }[1]
local pray2 = p:addParticles{ {x=0, y=0, size=5, color=0xaaaaaa, alpha=1} }[1]
 
local shapeid
stage:addEventListener(Event.MOUSE_HOVER,function (e)
	local mouse={x=e.x, y=e.y}

	-- reset all circles original colors
	for i = 1, #circlepts do
		p:setParticleColor(i, circlepts[i].color, 1)
	end

	-- gets the mouse nearest circle id
	local nearestpoint, npdistance = math.nearest(mouse, circlepts)
	shapeid=nearestpoint.id
	-- highlights circle if mouse is close
	if npdistance < circlepts[shapeid].radius + 48 then
		p:setParticleColor(shapeid, 0xffff00, 1)
	end

	-- checks if mouse is inside circle
	local inside = math.inside(mouse, nearestpoint)
	if inside < 0 then
		p:setParticleColor(shapeid, 0x00ff00, 1)
	end

	-- edge
	local d = math.edge(mouse, nearestpoint)
	p:setParticlePosition(pedge, d.x, d.y)

	-- raycast
	local r = math.raycast( -- origin, direction, shape
		{x=mouse.x, y=mouse.y},
		math.normalize({x=mouse.x-pixel:getX(), y=mouse.y-pixel:getY()}),
		circlepts
	)
	if r[1] then
		p:setParticlePosition(pray, r[1].point.x, r[1].point.y)
		p:setParticleColor(pray, p:getParticleColor(pray), 1)
	else
		p:setParticleColor(pray, p:getParticleColor(pray), 0)
	end
	if r[2] then
		p:setParticlePosition(pray2, r[2].point.x, r[2].point.y)
		p:setParticleColor(pray2, p:getParticleColor(pray2), 1)
	else
		p:setParticleColor(pray2, p:getParticleColor(pray2), 0)
	end
	-- a line
	raycast:clear()
	raycast:setLineStyle(5, 0xffffff, 0.5)
	raycast:beginPath()
	raycast:moveTo(mouse.x, mouse.y)
	raycast:lineTo(pixel:getX(), pixel:getY())
	raycast:endPath()
end)

Methods math.abs returns absolute value of v math.acos returns arc cosine value of v in radians math.asin returns arc sine value of v in radians math.atan returns arc tangent value of v in radians math.atan2 returns arc tangent value of v1/v2 in radians math.ceil returns smallest integer >= v math.clamp returns a number between min and max, inclusive math.cos returns cosine value of angle rad math.cosh returns hyperbolic cosine of v math.deg returns angle in degrees of radians rad math.exp returns e^v math.fft computes the discrete Fourier transform math.floor returns largest integer <= v math.fmod returns remainder of v1/v2 which is v1 - iV2 for some integer i math.frexp returns mantissa [0.5,1) and exponent values of v math.ifft computes the inverse discrete Fourier transform math.ldexp returns v1*2^v2 math.log returns natural logarithm of v math.log10 returns logarithm 10 of v math.max returns maximum in a list of one or more values math.min returns minimum in a list of one or more values math.modf returns the integer and fractional values of a number math.noise returns a perlin noise value math.pow returns v1 raised to the power of v2 math.rad returns angle in radians of degrees deg math.random returns random real [0,1-, integer [1,n] or real [1,u](with n=1- math.randomseed sets seed for pseudo-random number generator math.round returns integer with the smallest difference between it and the given number math.sign returns sign of v math.sin returns sine value of angle rad math.sinh returns hyperbolic sine of v math.sqrt returns square root of v math.tan returns tangent value of angle rad math.tanh returns hyperbolic tangent of v

Gideros specific methods math.length returns the length of a vector math.cross returns the cross product of two vectors math.dot returns the dot product of two vectors math.distance returns the distance between two points math.distances returns the distances between a point and a set of points math.nearest returns the nearest point from a list math.normalize normalize a vector math.raycast returns intersections between a ray and a set of shapes math.inside returns wether a point is inside a shape math.edge returns the nearest point on the edge of a shape Events Constants huge #INF pi 3.1415926535898

---

• Main Page
• Lua API
• Main API
• Plugins